今天將繼續說明除法器的運算過程與實現,篇幅比較長一點請見諒囉
在加減乘除的過程當中除法是最複雜的
因此還是先使用模仿紙筆的運算過程來看一下運算過程
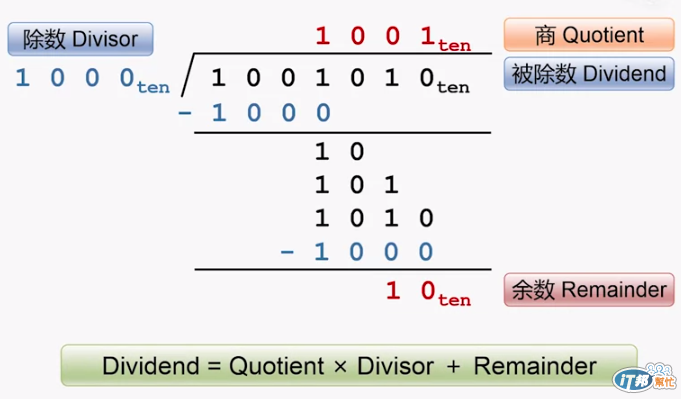
轉化成適合硬體實現的運算步驟可以得到下圖:
因此可以知道被除數若是八位寬,則除數和餘數都是四位
而被除數也可以看成是與餘數共享,另外除數和商數也是分別透過左移和右移來完成
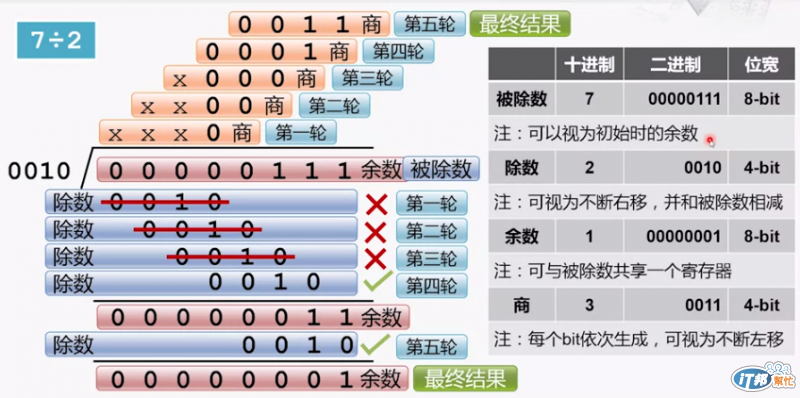
看了上圖就會發覺除法步驟真的是比較複雜了一點,接下來讓我們來看一下該怎麼實作:
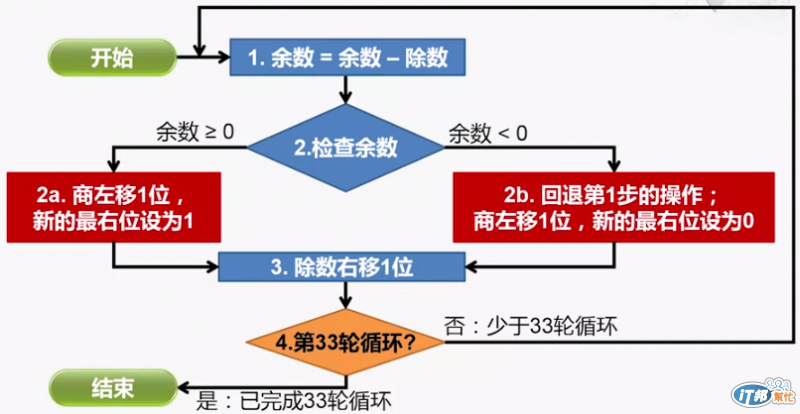
一樣我們可以得到除法器的通用計算流程,下圖是先暫用八位元來做示範
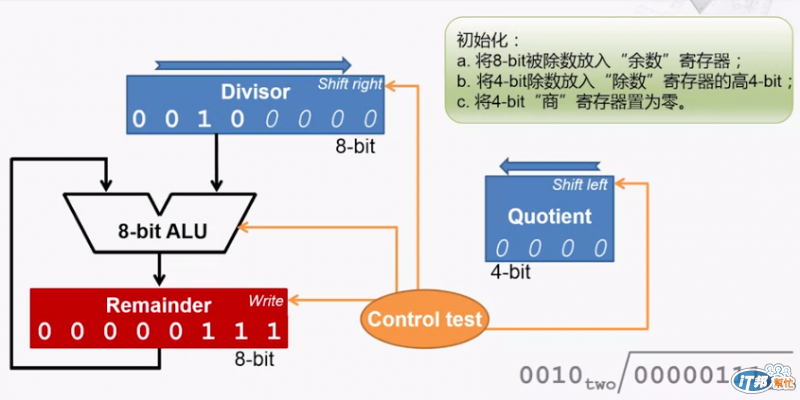
我們將會有:
初始化如下:
在經過第一輪餘數=餘數-除數之後,會檢查餘數是否小於零
這時候只要觀察最高為是否為一就可以知道了
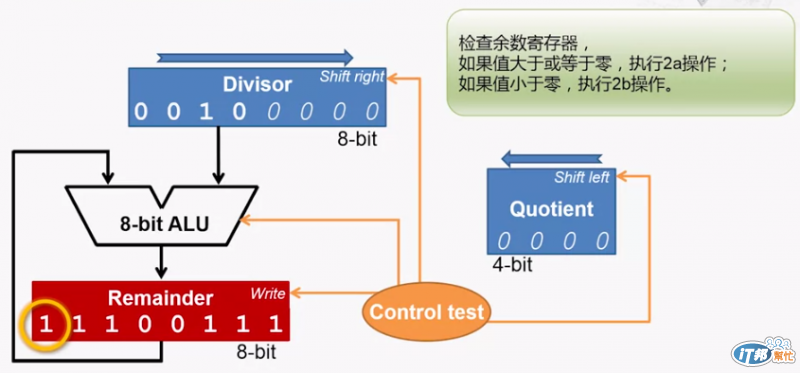
發現小於零表示實際上是不能減的,所以要將結果加回去
之後會右移除數,以及把商左移後設置為零

我們可以用一個表來表示各輪的動作:可以看到第四輪就不需要再回退了

這樣我們就可以完成一次的除法運算,並且得到商數和餘數了
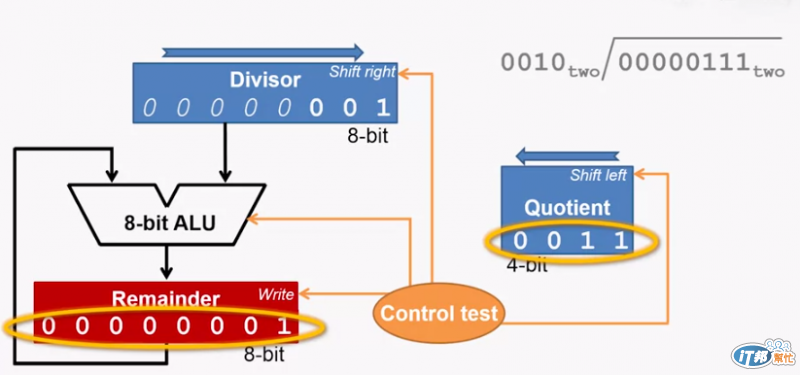
當然這個運算可以完成正數除以正數
但若除數與被除數一正一副,那餘數的判斷以及商數是多少呢
這就需要再後續考慮了,而除法器該如何優化,接下來也讓大家再自行參考老師的影片~!!
[心得]
三十天的鐵人賽到今天畫下句點~!!!
一開始覺得很困難,沒想到眨眼就結束了
在這段時間中跟著老師和馮紐曼一起了解計組的面貌其實也挺有趣的
從一開始的歷史到模型機最後到硬體電路實現,都讓我對這門資工基礎課程有了更進一步的掌握
學習還是會繼續,明年再見囉~!!!
